
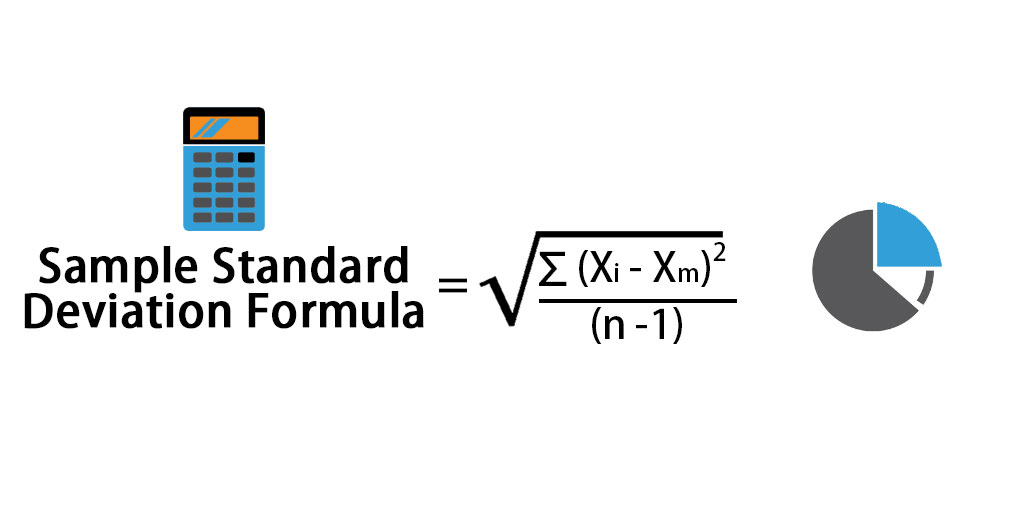

If you do so, you lose the type, since you need weights to be a vector, not a random object, to fit into a matrix or DataFrame. While using the type system to convey information about the type of weights sounds logical, I realized it does not suit much the case where weights are stored in a matrix or DataFrame, as a column, together with variables - which is the use case I think is the most common. That said, people only working with arbitrary weights with no precise meaning could still specify them as the most generic type, and they would get errors to prevent them from doing things that require more assumptions where applicable (like for corrected What kind of literature are you looking for? Something giving details about each type of weights are their use? (and the rest of the chapter, as well as the whole book) is a good reference for sampling weights. And while for example I would personally only need sampling weights, appears to be more familiar with inverse variance weights. ) Seriously, anybody dealing with weights will have to check what's the exact type of weights they have. an observation appearing twice in the replicate will have its weight doubled - such weights are sometimes shipped with survey data for privacy reasons when details about the survey design cannot be made It's not user-friendly, but it's just how the world works. I'm not sure they deserve their own type since they are actually just frequency weights (though sometimes combined with sampling weights, i.e. One may add "replicate weights" to the list: these simply reflect resampling replicates (e.g. "Analytic weights" are also called "precision weights" or "inverse variance weights"."Importance weights" should be the fallback type where others do not apply."Frequency weights" are also called "case weights" or "repeat weights".(More information is usually provided with surveys to compute statistics taking into account the survey design.) The only assumption which can be made with them is that they represent the inverse of the sampling probability, therefore their sum is the size of the target population. What they call "probability weights" are also called "sampling weights".I think you can find a good list here: and


 0 kommentar(er)
0 kommentar(er)
